أثناء سيري في الشارع والأرقام تحيط بي من كل جانب، إذا بي أجد ضجيجاً. يبدو أن هناك عددين يتشاجران. اقتربت مخترقاً صفوف الأرقام المصطفة تراقب المشهد. سمعت صوتاً عالياً يقول : “اسكت يا نص”.. كان العدد 2/5  يتشاجر مع العدد   ½، فالعدد 2/5  يقول أنه الأكبر ويسخر من “نص”، بينما  العدد ½  يقول أنه الأكبر. لم تدر الأرقام من تصدق؟

حينها فكرت.. ماذا تفعل حين تخبر طفلتين أنك تريد أن ترى من الأطول؟! ستتأكد بنفسك أولاً أنه لا يوجد ما يخرق القياس العادل. فتلك التي تمتليء عيونها لؤماً ستطلب منها الكف عن الوقوف على أطراف أصابع قدميها. أما الأخرى فستطلب أن تخلع الحذاء. ستكون حريصاً على التأكد أنهما بالفعل تقفان على مستوى واحد، فلا توجد من تعتمد على طول أصابع قدميها، ولا مجال لمن تعتمد على طول كعب الحذاء.

كذلك في الأعداد النسبية توجد أعداد مخادعة، تخطف نظرك للوهلة الأولى محاولة إقناعك أنها الأكبر. في هذه الحالة أيضاً يجب أن يقف العددين على مستوى واحد، فتكون المقارنة عادلة.

لذلك إن أردنا مقارنة 1/2   و 2/5  علينا أن لا نتسرع في الحكم، فنقول أن 2/5  أكبر من 1/2  لمجرد أنه أكبر في البسط والمقام معاً، فبمقارنة بسط العددين، سنجد 2 أكبر من 1، وبمقارنة مقام العددين سنجد 5 أكبر من 2.

دعنا لا نقع في خديعة الأرقام. فرقم 2 يقف على السلمة الخامسة لأنه مكتوب 2/5، بينما رقم 1 يقف على الثانية لأنه مكتوب 1/2 كما هو موضح بالشكل. لذلك يجب أن نضع العددين على نفس المستوى حتى تكون المقارنة منصفة بين الرقمين.  ألست كنت ستفعل نفس الشيء إن وجدت الطفلتين تقفان على سلمتين مختلفتين؟! كنت ستوقفهما على نفس درجة السلم لتحكم أيهما أطول.

الآن حتى نستطيع أن نعقد المقارنة علينا أن نختار سلمة واحدة يقف عليها العددان، أي نجعل العددين على قاعدة واحدة، أي مقام واحد، بحيث نتأكد على وجه الدقة أي العددين أكبر. ويجب أن تكون هذه السلمة بها شيء مشترك بين العددين، خاصية مشتركة تجمع العددين.

وأسهل طريقة لاختيار درجة السلم التي سنضع عليها العددين، هي أن نأخذ حاصل ضرب المقامين (2×5) لتكون هي السلمة الجديدة، أي أننا سنضع العددين على السلمة رقم 10. والقاسم المشترك هنا أن ال10 تقبل القسمة على كل من العددين 2 و 5

لكن كيف نجعل المقامات 10 للعددين؟! هل يمكن أن نغير المقامين لـ10 دون أن يؤثر ذلك على القيمة الفعلية للعددين؟!

كنت في حيرة.. ماذا أفعل الآن.. أتاني العدد 1 مسرعاً يشق صفوف الأرقام.. قال لي أنا سأحل لكم المشكلة. سألته: كيف؟ قال أنا عدد مرن جداً إن تم ضربي في أي عدد آخر لا يتأثر هذا العدد. فحاصل ضرب أي عدد في 1 يُنتج نفس العدد.

قلت له نعم.. أعلم ذلك  2×1= 2     3×1= 3 .. لكن ما علاقة ذلك بالمشكلة؟!

أجابني هذا هو حل المشكلة.. فأنا الذي سأجعل قاعدة العددين 10.

لكنني سأتنكر في شكل جديد، فأنا مرن قابل للتشكل، أنا 1 وأنا 5/5  وأنا 2/2

لمعت عيناي.. الآن فهمت أيها المنقذ الرائع..

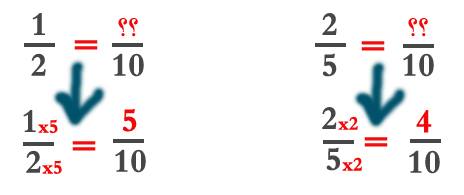
وكما هو موضح في الشكل أعلاه فإنه حتى نحول العدد ½  لعدد مقامه 10، سنضرب في 5/5، وحتى نحول العدد 2/5  إلى عدد مقامه 10 سنضرب في 2/2.

هنا تقوم الصيغة النسبية المتعددة للعدد (1) بعملية إنقاذ، فحاصل ضرب أي عدد  في (1)  هي نفس العدد. نستطيع أن نضرب أي عدد في (1) ونحن مطمئنين أن قيمته لن تتغير.. وبالفعل لم نكن نريد تغيير قيمة العددين الذين نقارن بينهما، كنا فقط نريد تغيير صورتهما مع احتفاظهما بنفس القيمة. وقد قام العدد (1) بدور رائع، حين أخذ مرة شكل (5/5)، وأخذ مرة أخرى شكل (2/2)، ليساعدنا في إعادة تعريف عددين ليس لهما مقام واحد.

الآن نعبر عن العددين ½  و 2/5  بصيغة جديدة هي 5/10، و 4/10 وبذلك نستطيع أن نضعهما على الدرجة العاشرة للسلم لنقارن بينهما بإنصاف. فـ 5 أكبر من 4، وهذا

يعني أن 5/10 أكبر من 4/10.. أي أن ½ أكبر من 2/5. على عكس ادعاء 2/5 بأنه الأكبر.

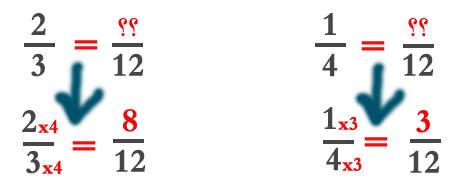
لم أكن أعلم قيمة العدد 1 قبل هذا الموقف. الآن يمكن أن يحل لنا مشاكل كثيرة. فللمقارنة بين 2/3 , 1/4 سنكون في حاجة إلى توحيد مقامهما للعدد 12 وهو حاصل ضرب المقامين (3×4).  هنا سينقذنا العدد 1 فحتى نجعل المقامات 12 سنضرب 2/3  في 4/4  ليكون الناتج 8/12  كما سنضرب العدد 1/4 في  3/3 ليكون الناتج 3/12 وبذلك يكون 8/12  أكبر من 3/12 أي أن 2/3 > 1/4 كما هو موضح في الشكل أسفل.

 الآن مستعيناً بمرونة العدد 1 يمكنك أن تعقد مقارنة بين أي رقمين بناء على مقارنة عادلة.. جرب الآن أن تقارن بين 4/6 , 1/2  .. أيهما أكبر؟!

هنا لا يشترط أن نضرب مقام الرقمين في 1، فيمكن بسهولة جعل مقام العدد 1/2 هو 6 ليكون على نفس الدرجة السادسة من السلم التي يقف عليها العدد 4/6.. يكفي أن نضرب 1/2 في 3/3 ليكون الناتج 3/6 وبالتالي يمكن مقارنته مباشرة بالعدد 4/6.. كما هو مبين بالشكل في الأسفل

أعلم أنك الآن تعشق العدد 1، بعد أن اكتشفت إحدى وظائفه العظيمة في إدارة عالم الأعداد، فهو العدد الذي يوجد القواسم المشتركة بين الأعداد، ولديه قدرة فذة على فض النزاعات. ما زال عالم الأرقام مبهراً.. يعلم الإنسان إن تأمل القواعد التي تحكمه.. تعلمنا الأرقام أن نعدل في مقارناتنا. فتكون المقارنة بين أشياء تجمعها أسس مشتركة، فلن نقارن بين النملة والتفاحة إلا إن حددنا مجال مقارنة مشترك، مثل اللون، فهذه بنية اللون وتلك حمراء اللون. لن نقارن بين الشعوب أو البلاد أو التجارب قبل أن نحدد مجال المقارنة المشترك. حينما يدعوك أحد إلى أي مقارنة لا منطقية قل له.. “فلنوحد المقام أولاً”

وائل عادل

06-05-2021