بينما أنا سائر في عالم الأرقام، لفتت انتباهي مجموعة من الأعداد النسبية تسير على رؤوسها وترفع أرجلها لأعلى. فالبسط تحول إلى مقام والمقام تحول إلى بسط. راقبت واحداً من هذه الأعداد الغريبة، فكان العدد 4/5 اقتربت منه وسألته: أنت 5/4 أم 4/5؟! فرد علي السؤال بسؤال: أنت ماذا ترى؟! قلت له: أنا أرى أنك 4/5، لكنك تتظاهر بأنك 5/4 حين تنقلب على رأسك… هل تريد أن تبدو أكبر من قيمتك الفعلية؟!
قال لي ببرود: يبدو أنك جديد في عالم الأرقام… أرجوك انصرف عني الآن فأنا على وشك إنهاء عملية قسمة!!
مشيت وأنا أفكر.. فلست أعرف كيف تتم قسمة الأعداد النسبية، لكنني أتذكر طريقة الضرب جيداً لأنها سهلة.. فلا يتطلب ضرب الأعداد النسبية نفس الجهد أو حتى مستوى التفكير المطلوب في جمعها أو طرحها. فلسنا في حاجة إلى توحيد المقام. ولكننا نضرب البسط في البسط والمقام في المقام كما هو موضح في الصورة.
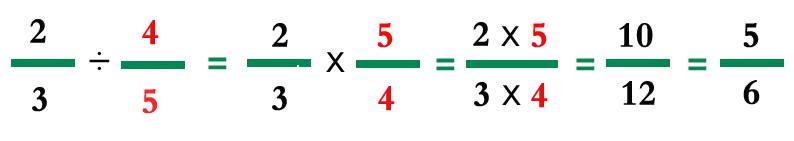
ولو تأملنا سنجد أن هذا ما يحدث أيضاً عند ضرب عددين مثل (3×6) فرقم 3 في صورته النسبية هو3/1 ، ورقم 6 هو 6/1 وبضرب بسطي الرقمين وضرب المقامين يكون الناتج 18 كما هو موضح في الصورة.
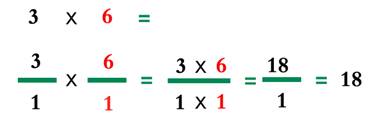
أما عملية القسمة فهي جديدة عليّ.. يجب أن أعود مجدداً إلى هذا الرقم المقلوب لأفهم منه ما يجري.. أسرعت مجدداً ناحيته.. وجدته عائداً، يعتدل ليقف وقفة طبيعية وينفض الغبار من عليه.. سألته: ما حكايتكم؟ لماذا أنتم مقلوبون هكذا وما علاقة هذا بالقسمة؟!
أشار إلى أرقام كثيرة مقلوبة قائلاً: أترى كل هذه الأعداد؟ إنها متجهة إلى ميدان القسمة، وهناك يتم ضربها في أعداد أخرى لتتوالد أرقام جديدة من ناتج القسمة؟
استوقفته قائلاً: مهلاً.. ضرب وقسمة أنا لم أفهم شيء؟ هل تمرون بعملية ضرب أم قسمة؟!
قال لي: اركب خلفي لأنني يجب أن ألحق عملية جمع في نهاية الشارع. وسأشرح لك في الطريق.. وبالفعل جلست على الشرطة التي تفصل البسط عن المقام وانطلق مسرعاً.
قال لي: ألا تعلم أن القسمة هي عملية ضرب مقلوب؟
سألته كيف؟ قال لي حين تقسم 6 على 3، فأنت فعلياً تضرب ال6 في 1/3 ، أي في مقلوب العدد 3، لذلك إن أردت قسمة أي رقم على 4/5، ستضرب هذا الرقم في 5/4.
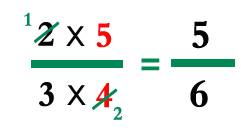
أخذت أجرب الموضوع.. فوجدت أن عملية القسمة أيضاً سهلة مثل الضرب، تكاد تكون هي نفسها. ومع التمرس يمكن أن نختصر مباشرة في عملية الضرب ذاتها، فرقم 2 في البسط و4 في المقام يمكن قسمة كل منهما على 2، واستكمال عملية الضرب كما هو مبين.
لا أنكر أن هذا السلوك الرقمي أثر في نظرتي لكثير من الأمور المعقدة، فبنظرة أولية إلى عملية قسمة 4/5 ÷ 2/3 نشعر بأن القسمة صعبة جداً. لكن بحركة رشيقة ومرنة من العدد يتبدل المشهد تماماً. فأنا لا أعرف القسمة لكنني أعرف الضرب. وهذا ما تفعله الرياضيات كثيراً في سلوكها الرقمي. أنها تعيد تعريف المشهد المعقد لنراه بسيطاً، وفي هذه الحالة تحديداً لم نكن بحاجة إلى أي أدوات خارجية تساعدنا في الحسابات.. كل المطلوب أن نمرن الأعداد على لعب الجمباز، لتمشي على رؤوسها..
واقتداء بالأعداد ذهبت إلى عملي سائراً على يداي معلقاً قدماي في الهواء. لعلي أرى المشهد مختلفاً.. وبالفعل حُلت بسبب ذلك أشياء كثيرة.. فالسيارات تنتظرني حتى أعبر الشارع ولا تفكر في دهسي مثل كل يوم. ولن أحتاج -بل لن أستطيع- أن أنظر في الهاتف كل 10 ثوان مثلما كنت أفعل من قبل. والأهم من ذلك.. لا مجال لرؤية وجوه الناس العبوسة وهي ذاهبة إلى أعمالها صباحاً.. فقط أرى أحذيتهم المسرعة.
وائل عادل
08-05-2021

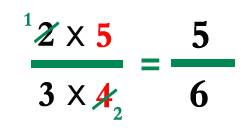
أضف تعليق